Если не понимаете, почему 52,4% — магическое число в ставках на спорт, не выйдете в плюс — так считал Эйнштейн

Альберт Эйнштейн назвал сложный процент самой могущественной силой во вселенной: «Кто понимает это — зарабатывает его; тот, кто не понимает — платит его».

Магические 52.4%

Экономика ставок на спорт устроена так, что для выигрыша в 10 долларов игрок должен рискнуть 11 долларами. Если ставка проходит, вы получаете 10 долларов плюс 11 поставленных. Если ставка проигрывает, букмекер забирает ваши 11 долларов.

Теперь проиллюстрируем эту концепцию с помощью формул, чтобы понять, откуда берется 52,4%.

Как устроен Вегас

Букмекер получает прибыль, когда проигрывает ставка клиента и когда он взимает маржу, заложенную в коэффициентах.

Математическое ожидание ставки (expected value, EV) рассчитывается по следующей формуле:

EV = W(p) — L(1-p)

• W = потенциальный выигрыш ($)
• p = вероятность выигрыша (%)
• L = потенциальный убыток или сумма риска для значения W ($)
• 1-p = вероятность проигрыша (%)

Вы рискуете 11 долларами, чтобы заработать 10, если ваша ставка пройдет.

Чтобы найти p, предположим математическое ожидание (или предполагаемая прибыль) равна 0.

$10p — $11(1-p) = 0

Выводим p:

• p = $11 / ($11+$10)
• p = $11 / $21
• p = 0.5238 или приблизительно 52.4%

0,524 — это значение, при котором ожидаемая прибыль равна нулю, то есть граница безубыточности.

Если бы букмекеры не брали 10% маржи от каждой ставки, бетторам нужно было выигрывать 50,1% ставок, чтобы получать прибыль.

Букмекер не зависит от результата матча

Мы можем расширить нашу формулу, включив в нее возможность получения прибыли, основанную на предпочтении игроков делать ставки на фаворита:

E (профит букмекера) = * (1+v) — **

• p = вероятность, что фаворит выиграет матч
• f = доля ставок на фаворита от суммы, поставленной на матч
• v = маржа букмекера

*доля ставок, в которых выигрывает букмекер . Это значение умножается на (1 + V), чтобы высчитать маржу

**выплата игроку, если букмекер проигрывает

Уравнение выше можно немного упростить:

E (профит букмекера) = (2 + v)*(f + p — 2pf) — 1

• p = вероятность победы фаворита
• f = доля ставок на фаворита ко всем ставкам на матч
• v = маржа букмекера

По словам автора книги «Фрикономика» Стивена Левитта: «Если вероятность победы двух команд равна (p = 0,5) либо объем ставок на эти команды равен (f = 0,5), размер прибыли букмекера сводится к банальной формуле v / 2. В таком случае букмекеру не важен исход матча, ведь они получают безрисковую прибыль, пропорциональную марже».

Чтобы обеспечивать себе прибыль, букмекеру не нужно предсказывать исходы игр точнее, чем это делают бетторы. Букмекеру нужно спрогнозировать предпочтения игроков, чтобы сбалансировать объем ставок на каждый исход.

Учитывая вышесказанное, давайте рассчитаем математическое ожидание (EV) справедливого подбрасывания монетки с точки зрения игрока:

EV = W(p) — L(1-p)

Стоит ли делать ставку на такое событие?

Пример 1.1

Вы рискуете 11 долларами, чтобы выиграть 10, если выпадет орел.

$10p — $11(1-p) = Математическое Ожидание (EV)

• p = 0.50 = вероятность выигрыша ставки (выпадает орел).
• 1-p = 0.50 =вероятность проигрыша ставки (выпадает решка).
• $10 = сумма выигрыша игрока в случае выпадения орла.
• $11 = сумма, которой игрок рискует, чтобы выиграть 10 долларов.

(10* 0.50) — (11* 0.50) = -0.5 = Математическое Ожидание (EV)

Чтобы рассчитать ожидаемый возврат инвестиций (ROI), разделим математическое ожидание на сумму, которой игрок рискует:

= ROI

(-0.50/11) = -4.55%

Очевидно, что принимать такое пари не стоит. Математическое ожидание отрицательное, следовательно, если подбрасывать монетку с теми же вероятностями, ваш банкролл уменьшится на 4.55%.

Теперь представим сценарий с шулерской монеткой, при которой вероятность орла 52,4% (p = 0,524), вероятность решки — 47,6%. Подставим цифры в нашу первую формулу, математическое ожидание (EV) будет равно нулю. В долгосрочной перспективе вы не потеряете деньги, но и не заработаете ничего.

Точка безубыточности

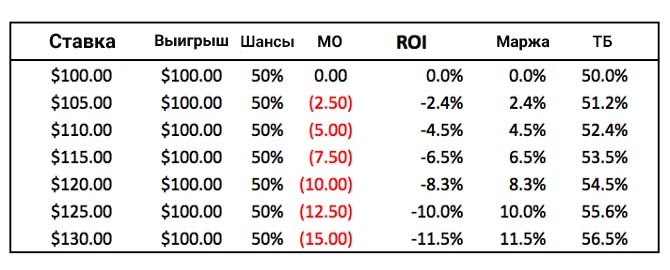
• Шансы = вероятность выигрыша игрока
• МО = математическое ожидание игрока;
• Маржа = маржа букмекера
• ТБ = точка безубыточности игрока или процент ставок, которые нужно выиграть, чтобы достичь безубыточности

Эффективный способ обанкротиться…

Отношение ROI к марже букмекера при подбрасывании монетки.

Как букмекеры получают безрисковую прибыль — маржа

В теннисном матче между спортсменами А и Б половина ставок пришлась на П1 и половина на П2. Те, кто ставил на А и кто ставил на Б, рискуют 11 долларами, чтобы выиграть 10. Как бы ни закончился матч, чистая прибыль букмекера — 1 доллар с каждой ставки. Это и есть его маржа.

Итого:

• Поклонники А рискуют 11 долларами.
• Поклонники Б рискуют 11 долларами.
• Букмекер собирает 22 доллара на каждую пару игроков.

После матча букмекер оставляет себе 1/22 суммы ставок или 0,045 (4.5%), выплатив тем, кто ставил на победителя их 11 долларов плюс 10 долларов выигрыша.

Как разобраться в вероятностях и пороговых значениях

Математическое ожидание / Сумма ставки $ = Возврат инвестиций

ROI лучше представить как отношение ожидаемой прибыли к сумме ставки, только на долгой дистанции.

Если вы хотите быть успешным на дистанции, нужно научиться просчитывать вероятности и ставить только тогда, когда шансы выше, чем оценивает букмекер, а математическое ожидание больше нуля.

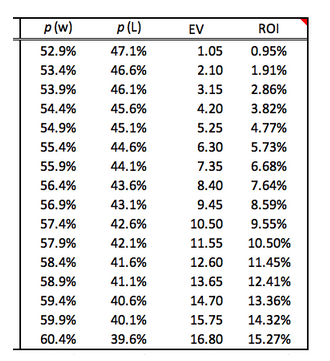
Таблица расчета математического ожидания

Рискуешь 110 долларами, чтобы выиграть 100

Использовать, когда вероятность выигрыша > 52.4+n .

p(w) = 52.9%

Мат. ожидание = (0.529 * $100)-(0.471 * $110) = 1.05, ROI = 1.05/$110 = 0.95%

• p(w) — вероятность выигрыша
• p(l) — вероятность проигрыша
• EV — математическое ожидание
• ROI — возврат инвестиций

Перевод статьи Стивена Левитта на сайте medium.com.